Esta guía trata acerca de campos escalares y vectoriales, que gráficamente serían superficies en R³. Es muy interesante este concepto ya que con esto se podría describir todos los objetos en el espacio como funciones matemáticas: por ejemplo las cosas que nos rodean podríamos describirlo con funciones y realizar cálculos y operaciones a partir de ellas.

Tabla de contenidos

Enlaces

📄 Ver/Descargar PDF Resumen

📄 Ver/Descargar PDF Resoluciones - Conjuntos de Nivel, Límites y Continuidad de Campos

📄 Ver/Descargar PDF Resoluciones - Derivadas Multivariables

📄 Ver/Descargar PDF Resoluciones - Diferenciabilidad

📄 Ver/Descargar PDF Resoluciones - Superficies

Última actualización: 01/05/2025

Consejos

Videos para familiarizar conceptos

Técnicas de resolución de límites

Para resolver los límites propuestos en esta guía que en gran mayoría son divisiones polinómicas, se pueden aplicar las siguientes técnicas:

  • Probar la inexistencia del límites \(\arrowright\) probar por curvas. Si el límite existe, es único.
  • Probar función acotada y que tiene forma \(0 \cdot acotado\)
  • Cambios de variable
  • Simplificar términos
  • Parametrización
  • Divisiones polinómicas

Técnicas para probar diferenciabilidad

  • Probar por definición de diferenciabilidad
  • Probar clase de función: si pruebo que función es de clase \(C¹\) entonces es diferenciable
  • Probar que no es diferenciable
    • Si no es continua
    • Si no es derivable: por ejemplo si no existe derivadas parciales o no son continuas

Conceptos interesantes

Gráficos de campos escalares y superficies

Los gráficos de las funciones de campos escalares generalmente son en una dimensión más al dominio \(D\) en la que están definidos. Por ejemplo si tengo una función escalar \(f(x,y)\) con dominio en \(R²\), su gráfico tendría que ser en \(R³\) (algo de este estilo: \(G_f=\left \{(x, y, z)\in R³ / z=f(x,y)\right \}\)) y eso podría llegar a formar una superficie. Esto se ve reflejado con el gráfico de las cuádricas que son todas representaciones gráficas de funciones escalares, teniendo en cuenta la restricción de dominio en algunos casos.

  • Paraboloide = \(P: \left \{(x, y, z)\in R³, z=f(x,y)=x²+y² \right\}\)
  • Conos \(C: \left \{(x, y, z)\in R³, z=\sqrt{x²+y²} \lor z=-\sqrt{x²+y²}\right \}\)

Un paraboloide cute

Gráficos de conjunto nivel

Los gráficos de conjunto nivel pueden llegar a ser curvas en la dimensión en la que están definidas (ojo con esto si pide graficar).

La 4ta dimensión

En física o ciencias en general se llama al tiempo \(t\) como la cuarta dimensión. Podemos observar esto en una ecuación de la trayectoria de un objeto cualquiera en el espacio:

\[\vec{R}: \left \{ (x(t), y(t), z(t), t), t \in R \right\}\]

La ecuacion es una curva en R³. Pero, ¿Qué pasa si quiero visualizar el tiempo \(t\) en un mismo gráfico? La 4ta dimensión se puede pensar hipercubo (un cubo dentro de otro xd), donde los cubos son el espacio \(R³\) y las líneas diagonales son el tiempo que une un espacio al otro.

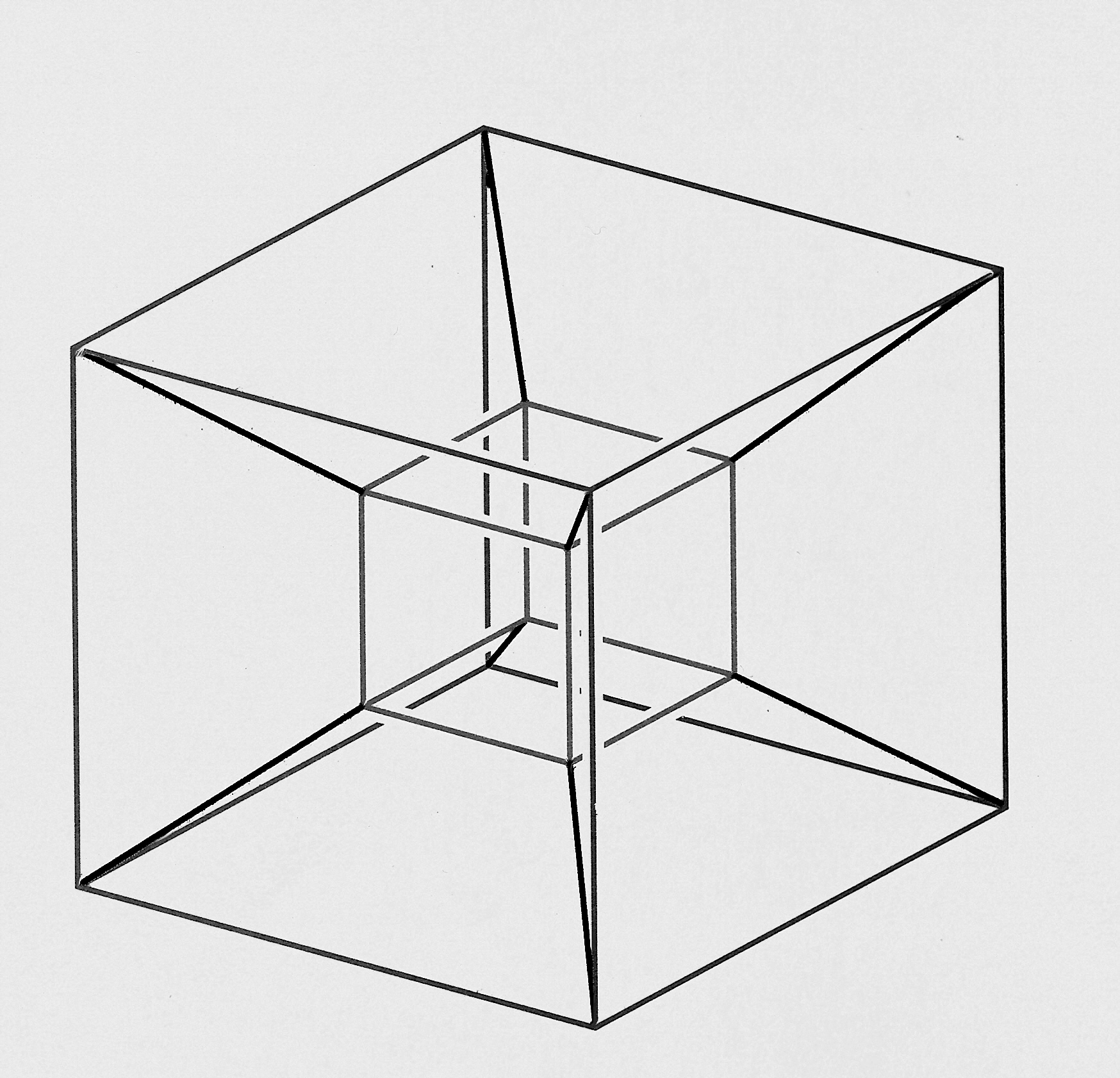
Hipercubo

Aunque no los podamos ver, es bueno tener en cuenta este concepto tanto para física o computación. Los LLMs (GTPs) trabajan con vectores de más de miles de dimensiones por ejemplo.

Planos tangentes

  • Las derivadas parciales \(f_x\) \(f_y\) sacan vectores tangentes ‘canónicos’ a la superficie a estudiar. Entonces con los vectores hallados puedo armar un plano tangente a un punto cualquiera de la superficie, ya que todas las otras tangentes serían combinaciones lineales de las canónicas.

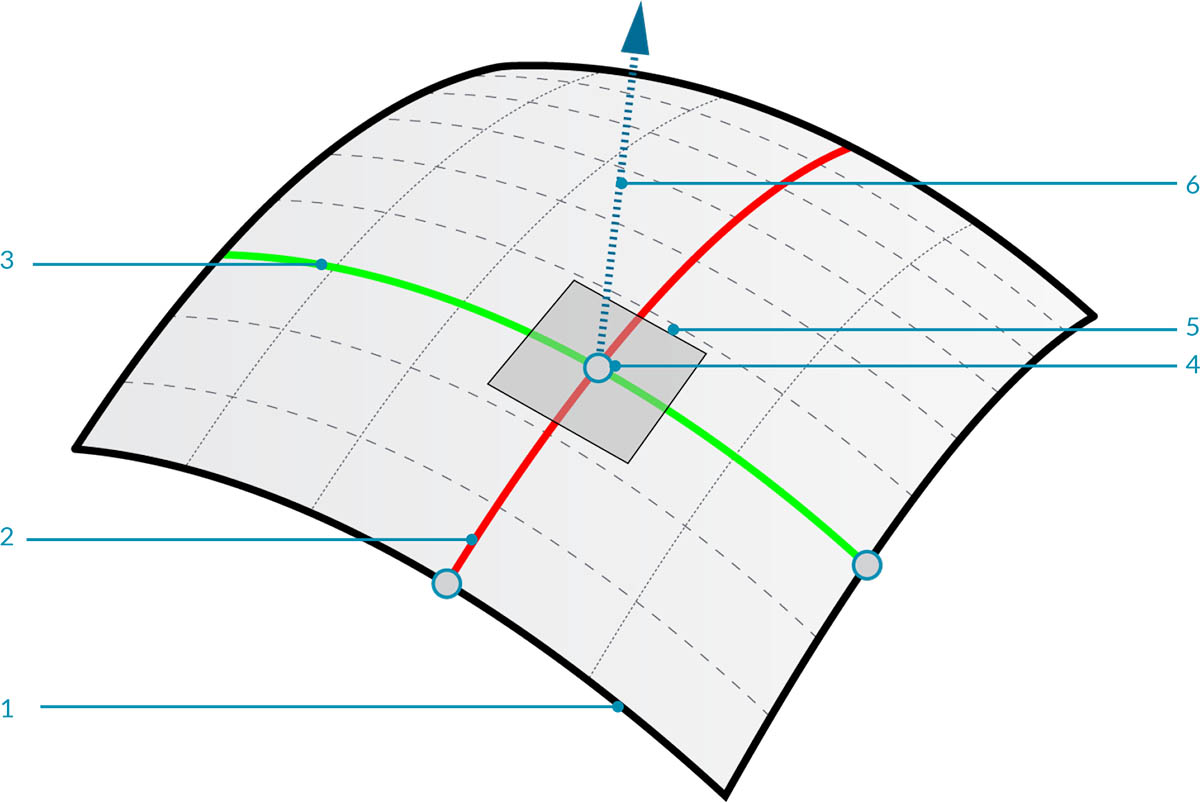
Superficie con plano tangencial

Ejercicios con procedimiento

Ejercicio 2b

Grafique, si quedan definidos, el conjunto de nivel 0 y el conjunto de nivel 4 de:

\[f(x,y)=sen(y-x)\]

En general, el conjunto nivel k (\(N_k\)) es el conjunto de puntos del dominio donde la imagen de la función sea k. Entonces hallar \(N_k\) es hallar \((x, \dots ,x_n) \,/ \,f(x,\dots x_n)=k\).

Primero buscamos el dominio de \(f(x,y)=sen(y-x)\) que son todos los \((x,y)\in R²\). Como es una función trigonométrica, sabemos que es periódica y acotada. La función seno varía entre [0,1] por lo que el conjunto nivel \(k\) tiene que estar en ese intervalo: \(k\in [0,1]\). Con esto ya descartamos el conjunto nivel \(k=4\) (\(N_4=\emptyset\)).

Buscamos Conjunto nivel \(k=0\) por medio de la siguiente ecuación y despejamos:

\[sen(y-x)= k = 0 \\ y-x = arcsen(0) \\ y-x = \lambda \pi, \, \lambda \in Z\\ y = x+\lambda \pi, \lambda \in Z\]

Acordarse de que seno es una función periódica por lo que hay distintos ángulos resultantes si aplico arcoseno

Finalmente nos quedan ecuaciones de rectas que son variacion de la recta identidad \(y=x\) sumando la cantidad de pis (\(\pi s\) xd) según la periodicidad en ese ángulo:

\[\dots \\ \lambda = 0, \, y=x \\ \lambda = 1, \, y=x+\pi \\ \lambda = -1, \, y=x - \pi\\\ \dots\] \[N_0=\left\{(x,y)\in R² /\,\, y=x+\pi\lambda, \, \lambda \in Z \right \}\]

Ejercicio 3 - Límites

Ejercicio 3h

\[\lim_{(x,y)\to(0,0)} \frac{sen(x²-y²)}{x-y}\]

Si evaluamos el límites por familia de curvas, observamos que tanto por rectas \(y=mx\) como por parábolas \(y=kx²\) dan 0. Así que podemos sospechar de que si el límite existe, es 0.

Por otro lado, la función en sí, el término \(x²-y²\) es una diferencia de cuadrados \(x²-y² = (x+y)\cdot(x-y)\) pero reescribirlo así adentro de la función de seno no tiene sentido xd. Lo que sí podemos destacar es que si lo escribimos así \(sen((x+y) \cdot (x-y))\) se repetiría el término \((x-y)\) del denominador. Entonces por qué no transformar el denominador en la diferencia de cuadrados para llegar a algo parecido a \(sen(x)/x\):

\[\begin{align*} \lim_{(x,y)\to(0,0)} &\frac{sen(x²-y²)}{x-y} \\ \lim_{(x,y)\to(0,0)} &\frac{sen(x²-y²)}{x-y} \cdot \frac{x+y}{x+y}\\ \lim_{(x,y)\to(0,0)} &\frac{sen(x²-y²)}{x²-y²} \cdot (x+y)\\ \end{align*}\]

Una vez que llegamos a esta expresión podemos aplicar la siguiente propiedad/identidad \(\lim_{x\to 0}\frac{sen(x)}{x} = 1\) y resolvemos el límite:

\[\lim_{(x,y)\to(0,0)} \underbrace{\frac{sen(x²-y²)}{x²-y²}}_{\to 1} \cdot \lim_{(x,y)\to(0,0)}\underbrace{(x+y)}_{\to 0 } = 1 \cdot 0 = 0\]

Ejercicio 3n

\(\lim_{(x,y)\to(1,1)} \frac{2y²-x²-xy}{y-x}\)

El límite presenta indeterminación \(\frac{0}{0}\) y se puede resolver de varias maneras: realizando la división polinómica (coeficiente de numerador mayor que denominador), o factorizando y simplificar términos. En este caso simplificar es más fácil de ver creo:

\[\begin{align*} \lim_{(x,y)\to(1,1)} &\frac{2y²-x²-xy}{y-x} \\ \lim_{(x,y)\to(1,1)} &\frac{y²+y²-x²-xy}{y-x} \\ \lim_{(x,y)\to(1,1)} &\frac{(y²-x²)+(y²-xy)}{y-x} \\ \lim_{(x,y)\to(1,1)} &\frac{(y+x)(y-x)+y(y-x)}{y-x} \\ \lim_{(x,y)\to(1,1)} &\frac{(y-x)[(y+x) + y]}{(y-x)} \\ \lim_{(x,y)\to(1,1)} &(y+x) + y = 3 \end{align*}\]