En mi opinión la mejor guía hasta ahora. Casi todos los conceptos son relacionados a física.
Recordatorio
Las integrales no se utilizan sólamente para calcular áreas y volumenes. Esto me había confundido mucho cuando vi por primera vez el cálculo de la longitud de un segmento (parte de una curva).
Recordar que la integral es una sumatoria al infinito y continua:
\[\int_{a}^{b} f(x) dx = \lim_{n \to \infty}\sum_{i=1}^{n} f(x_i) \cdot \Delta x\]Básicamente la suma de Riemann pero al infinito y valores continuos.
Tabla de contenidos
Enlaces
📄 Ver/Descargar PDF resoluciones - Integrales línea y curvilínea
Videos para familiarizar conceptos
Recomiendo los videos del profe Maulhardt que explica muy bien los conceptos y no sólo fórmulas. Enlaces
Mis interpretaciones de conceptos
Integral Campo Escalar sobre Curva
Esta integral se pude interpretar de dos maneras:
- Interpretación física
En muchos ejercicios de la guía se utiliza esta integral para calcular la masa de un objeto. Normalmente te dan una función \(\delta(x)\) que nos da la densidad en cada punto de la curva.
Para encontrar la masa total, tendríamos que sumar todas las masas de manera continua e infinitamente de la curva. Como la densidad es masa por unidad de volumen, en este caso el volumen sería la longitud de la curva, ya que trabajamos con una línea. Matemáticamente esto se expresa como el límite de la suma:
\[\lim_{n \to \infty}\sum_{i=1}^{n} \delta(x_i) \cdot \Delta l_i\]Donde \(l_i\) es la longitud del segmento pequeño de la curva.
Y como mencioné al principio, esta sumatoria infinitedecimal es una integral definida:
\[\int_{a}^{b} \delta(g(t)) \cdot |g'(t)| dt = \lim_{n \to \infty}\sum_{i=1}^{n} \delta(g(t_i)) \cdot \Delta l_i\]- Interpretación geométrica y analítica
Desde un punto de vista más abstracto, esta integral puede interpretarse como el cálculo del área bajo la función evaluada a lo largo de una curva. Es decir, estamos midiendo el área que queda “entre” la curva y la función compuesta con dicha curva.
Esto equivale a integrar la función a lo largo de la trayectoria de la curva, lo que generaliza el concepto clásico de “área bajo la curva” para funciones definidas sobre trayectorias curvas en un espacio.
Si queremos podemos llevar este concepto a un entorno de \(R²\) más familiar. El área debajo de una curva como la conocemos en análisis I, es un caso particular de esta integral curvilínea. En este contexsto el diferencial dx puede interpretarse como la tangente en cada punto de la curva parametrizada por \(g(t)=(t, 0)\) ya que el eje x puede representarse mediante esa curva.
Soy muy malo redactando ahí dejo un gráfico de lo que estoy diciendo
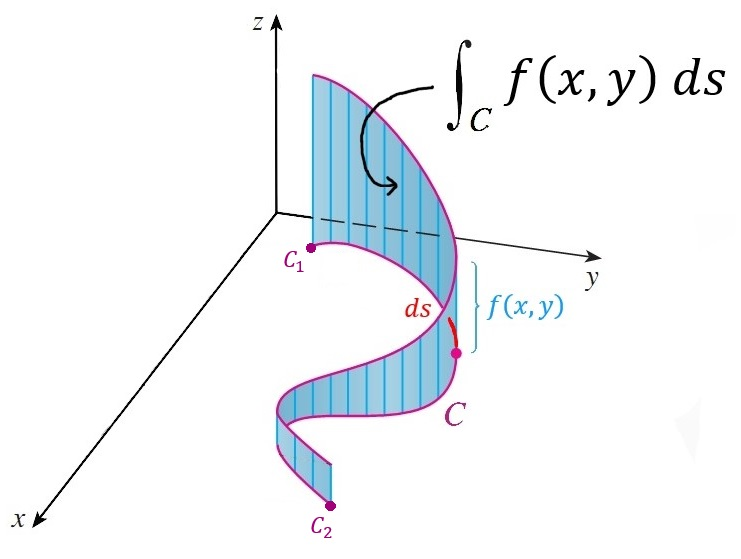
Integral de línea/curvilínea
La imagen fue sacacada de este post. Explica muy bien los distintos tipos de integrales y su uso.
Integral Campo Vectorial sobre Curva
Este concepto es muy importante para la física y la ingeniería en general. Podemos pensarlo como la trayectoria de un objeto siendo influenciado por fuerzas externas de su entorno y espacio en el que se encuentra.
La fórmula matemática es similar a integrales de línea para campos escalares, sólo que en este caso realizamos producto escalar entre el campo vectorial y el vector tangente a la curva:
\[\int_{a}^{b} \vec{F}(\vec{g}(t))\cdot \vec{g}\,'(t) \,dt\]Es necesario mencionar que la dirección y el sentido de los vectores son muy importantes acá; por lo que no es lo mismo recorrer la curva en un sentido que en el otro, ya que eso afecta directamente al resultado de la integral.
Un ejemplo visual de un campo vectorial y una curva cerrada es la siguiente:
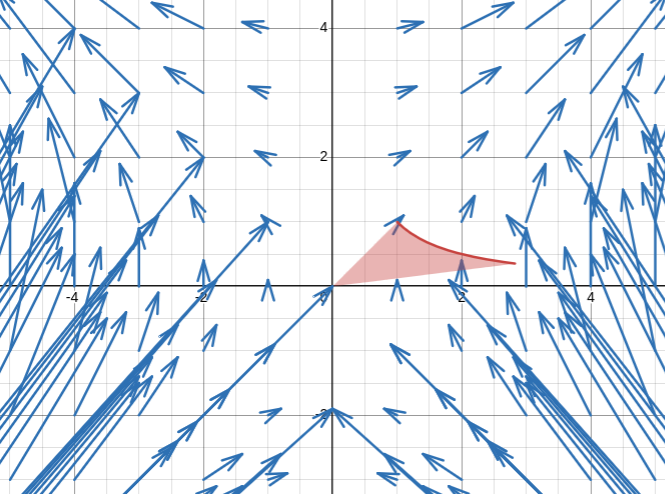
Campo vectorial (azul) y curva cerrada (frontera de región roja)
Para entender mejor podemos pensarlo así:
El campo vectorial representa las fuerzas del contexto o el espacio, que puede ser un fluido, el viento que sale de un ventilador, o incluso un campo electromagnético. Mientras que la curva representa la trayectoria que sigue una partícula u obejeto. A medida que se recorre la curva (variando el paámetro en la ecuación de curva), el objeto se va desplazano y siendo influenciado por el campo.
Teniendo esto en cuenta, justifica lo mencionado anteriormente que no es lo mismo moverse en un sentido o en otro.
Esto tiene aplicaciones muy prácticas. Por ejemplo, si estoy en un barco o submarino, y conozco la fórmula matemática y el comportamiento de una corriente marina, puedo aprovechar eso y elegir la mejor ruta para llegar rápido o evitar rutas que nos frene (osea básicamente si estuviera en el Titanic hubiera prevenido el iceberg y por eso es importante aprender analisis 2).
Y físicamente hablando, el resultado de esta integral nos da la circulación del campo sobre la curva, que se inhterpreta como el trabajo que realiza el campo sobre la partícula al recorrer esa trayectoria.
Líneas de campo
Las líneas de campo \(\vec{g}(t)\) tienen que cumplir con la condición
\[\vec{F}(\vec{g}(t)) = \vec{g}\,'(t)\]Osea básicamente es una trayectoria donde su velocidad coincide con la aplicación de la fuerza en todos los puntos. Quiere decir que si quiero ir por la ruta más rápida y sin poner energía podría ir por una línea de campo ya que me llevaría por el campo vectorial.
Para encontrar una línea de campo de un campo vectorial se utilizan ecuaciones diferenciales.
Función potencial
Punto de vista físico
Una forma de ver función la potencial es pensandolo desde un punto de vista físico y teniendo en cuenta los trabajos de fuerzas conservativas y no conservativas en el enunciado y ver si se puede aplicar el teorema de conservacion de energía:
\[\Delta Ep = 0\]Punto de vista geométrico y analítico
En el caso particular de los campos vectoriales de dos variables \(\vec{F}(x,y)\) podríamos pensarlo como si fuera el gradiente de una función escalar de dos variables \(f(x,y)\).
Si grafico esa función escalar de la siguiente manera \((x,y,f(x,y))\) obtengo una superficie en R³. Lo que es interesante es que ahora podemos observar en dónde la superficie crece y en dónde decrece, coincidiendo exactamente con el gráfico del campo vectorial en R². Esto está directamente relacionado porque si \(\vec{F}(x,y)\) es el gradiente de la superficie entonces indica la dirección y magnitud de los planos tangentes a la superficie (la pendiente de la superficie).
Campo vectorial (derecha) y potencial escalar correspondiente (izquierda)
Mezclando esto un poco con física podemos pensar lo siguiente: suponiendo que tengo un objeto ubicado a una altura de una superficie, y no hay fuerzas no conservativas presentes, si lo dejo caer, se va a conservar la energía entre puntos de misma altura en la superficie (equipotencial).
Actualizacion: encontre un video que explica lo mismo pero mejor
